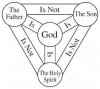
大家知道'三位一体'。它的文字描述是圣父、圣子和圣灵合为一体。其数学表达式为3的0次方等于1。这里来讲讲它的纯粹的图形以及立体表示。
先拿出张纸和笔。在纸上画一个等边三角形,亦即正三角形。它是三个边长相等的三角形,其三个内角也是相等的,为60度。
然后在三角形的中心画个点,再从这个中心点画三条直线分别到正三角形的各个角点。这样,一个表示'三位一体'的平面图形就画出来了。
现在来看这个2维的平面图形,它有4个点,其中一个点在中心。它有6条边,其中从中心向外的3条线段长度相等,但是不等于另外3条边(它们是正三角形的边)。这个图形还有4个三角形,其中的一个外围的大的等边三角形包括了其内部的三个小三角形。这三个小三角形是相等的,是等腰三角形,却不是等边三角形(等边三角形是等腰三角形的一个特殊形式)。
问题来了,如何化解等腰三角形为等边三角形呢?
再看看3维立体的情形吧。一个正三角体,如同埃及的金字塔的形状。它是立体的,有4个相同面积的正三角形,有4个点,还有有6条长度相等的棱边。
把它放在平面上,有一个面为正三角形的底面,其余3个正三角形是斜面,共交合在一个顶点上。
现在从顶上往下看,也就是制图学的一个名词,叫俯视图。这个俯视图就前面所说的2维的'三位一体'的平面图。所以,表示'三位一体'的3维立体形状是正三角体。
这里讲解了可以表示'三位一体'的2维平面图和3维正三角体,以及它们之间的关系。
至于其它的意义,就各抒己见吧。
先拿出张纸和笔。在纸上画一个等边三角形,亦即正三角形。它是三个边长相等的三角形,其三个内角也是相等的,为60度。
然后在三角形的中心画个点,再从这个中心点画三条直线分别到正三角形的各个角点。这样,一个表示'三位一体'的平面图形就画出来了。
现在来看这个2维的平面图形,它有4个点,其中一个点在中心。它有6条边,其中从中心向外的3条线段长度相等,但是不等于另外3条边(它们是正三角形的边)。这个图形还有4个三角形,其中的一个外围的大的等边三角形包括了其内部的三个小三角形。这三个小三角形是相等的,是等腰三角形,却不是等边三角形(等边三角形是等腰三角形的一个特殊形式)。
问题来了,如何化解等腰三角形为等边三角形呢?
再看看3维立体的情形吧。一个正三角体,如同埃及的金字塔的形状。它是立体的,有4个相同面积的正三角形,有4个点,还有有6条长度相等的棱边。
把它放在平面上,有一个面为正三角形的底面,其余3个正三角形是斜面,共交合在一个顶点上。
现在从顶上往下看,也就是制图学的一个名词,叫俯视图。这个俯视图就前面所说的2维的'三位一体'的平面图。所以,表示'三位一体'的3维立体形状是正三角体。
这里讲解了可以表示'三位一体'的2维平面图和3维正三角体,以及它们之间的关系。
至于其它的意义,就各抒己见吧。